محیط اطراف ما پر از خطوط و شکل های هندسی مختلف است که با هر کدام از آنها دارای خصوصیات و شرایط خاص خود هستند که شناخت آنها خالی از لطف نیست. از طرفی یک از مهمترین و اساسی ترین مباحث ریاضی و فصول کتاب همین موضوع هندسه و مبانی مرتبط با آن میباشد. طراحان سوالات ریاضی خیلی اوقات هم مباحث دیگر را با هندسه مخلوط می کنند و شما تا زمانی که مباحث پایه و اساسی هندسه را ندانید نمیتوانید سوال مورد نظر را حل کنید. به همین خاطر ما در این مقاله تلاش میکنیم تا مباحث مربوط به هندسه ریاضی که در مقطع ابتدایی برای ما و فرزندتان مفید و لازم هستند را برای شما با توضیح کامل بیان کنیم.
خط
اجتماعی از نقاط که آنقدر به هم نزدیک میشوند که پیوسته شده و یک خط را تشکیل می دهند. یک خط از دو طرف باز است و ما هیچ محدودیتی در مورد امتداد آن از دو طرف نداریم.
نیم خط
خطی که از یک طرف بسته شود نیم خط گفته می شود. نیم خط ازیک سو باز و بدون محدودیت و از سمت دیگر با محدودیت و عدم امتداد مواجه است. پس ما آن سوی نیم خط که بسته شده است را نمی توانیم امتداد بدهیم.
پاره خط
به خطی که از دو طرف بسته شده باشد و محدوده و اندازه مشخصی دارد پاره خط میگوییم. چون پاره خط بسته شده است قابلیت اندازه گیری دارد.
زاویه
دو خط فرضی با هر ویژگی ممکن است در یک نقطه به هم برخورد کنند و در نقطه برخورد بسته شوند و تشکیل دو نیم خط را بدهند که قرار گیری خاصی نسبت به یکدیگر دارند. پس به دو نیم خط که یکدیگر را در نقطه خاصی قطع کرده اند، زاویه میگویند. انواع زاویه داریم که در زیر آنها را توضیح میدهیم:
- زاویه تند: زوایای کوچکتر از 90 درجه هستند.
- زاویه راست یا قائمه: به زاویه ای که اندازه ان 90درجه باشد گفته می شود.
- زاویه باز: به زوایای بیشتر از 90 درجه می گویند.
- زاویه نیم صفحه: به زاویه 180 درجه گفته می شود.
مطلب پیشنهادی: شیرین کردن ریاضی برای کودکان
انواع اشکال هندسی
شکل هایی که از برخورد خطوط مختلف با یکدیگر ایجاد شده اند و هر کدام ویژگی ها و شرایط خاص خود را دارند.
نیمساز زاویه
به نیم خطی که زاویه را به دو زاویه مساوی تقسیم می کند، نیمساز آن زاویه گفته می شود. پس هر زمان بگویند خطی نیمساز یک زاویه است، ما به آسانی حدس خواهیم زد که زوایای دو طرف نیمساز با هم مساوی هستند.
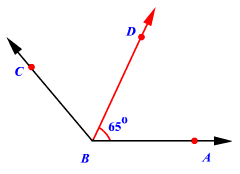
ارتفاع
پاره خطی که از یک راس آغاز می شود و بر ضلع مقابل آن راس عمود میشود ارتفاع گفته میشود. پس همیشه ارتفاع بر قاعده عمود است و با آن یک زاویه 90 درجه می سازد.
قطر
پاره خطی که دو گوشه یا راس رو به روی هم در شکل را به هم وصل می کند، قطر نامیده می شود. قطر راس های مجاور را هم به یکدیگر وصل نمی کند. در شکل زیر یکی از قطرهای مربع نشان داده شده است.
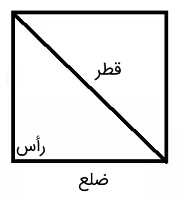
نکته: دایره بینهایت قطر دارد. زیرا بینهایت نقطه مقابل هم دارد که میتوانند به یکدیگر وصل شوند.
نکته: مثلث قطر ندارد. در تعریف گفتیم که قطر گوشه هایی که در مجاورت یکدیگر هستند را به هم وصل نمی کند و در مثلث هیچ دو گوشه ای که با هم مجاور نباشند پیدا نمی شود پس قطری ندارد.
تعریف محیط و مساحت اشکال هندسی
محیط
محیط به معنای دور تا دور شکل می باشد. به این نحو که ما یک نخ برداشته و آن را به طور کامل دور یک شکل بپیچیم وسپس نخ را بلند کرده و اندازه آن را به کمک خط کش بگیریم به این نحو محیط شکل به دست خواهد آمد. واحد اندازه گیری محیط همان متر یا سانتی متر است که بستگی به واحد اندازه گیری دارد.
مساحت
مساحت به معنای سطح پوشانده شکل است. اگر ما شکلی داشته باشیم و بخواهیم آنرا با مربع های کوچک با ضلع یک سانتی متر پر کنیم تعداد آن مربع ها مساحت شکل را به ما می هد. پس مساحت همان سطحی است که توسط مربع ها پوشانده می شود. همچنین واحد اندازه گیری مساحت شکل ها سانتی متر مربع و یا متر مربع است.
شکلهای هندسی و ویژگی های آن ها
در این بخش ما تک تک شکل های هندسی که در مقطع ابتدایی ممکن است مورد استفاده باشند می پردازیم و نکات مهمی را در مورد آنها بیان می کنیم که در مقطع ابتدایی بسیار مهم هستند.
مثلث
ساده ترین و اولین شکل هندسی که از سه پاره خط تشکیل می شود. با اتصال این پاره خطها به یکدیگر سه زاویه تشکیل می شود. پس هر مثلث سه ضلع و سه زاویه دارد. دانش آموزان پایه اول ابتدایی به مثلث، سه گوش هم می گویند. مجموع زوایای داخلی مثلث 180 درجه می باشد که باید در حل تمرین های کتاب از این نکته استفاده شود. مثلث دارای سه ارتفاع است که از هر کدام ازگوشه ها به ضلع روبرو عمود شده است که گاهی درون شکل است گاهی هم در خارج شکل می افتد. سه نوع خاص مثلث هم داریم که در زیر آنها را توضیح میدهیم.
مثلث قائم الزاویه: ویژگی مهم این مثلث وجود یک زاویه قائمه میباشد. ضلع روبرو در این مثلث نیز وتر نامیده می شود. درحل بسیاری از سوالات این نکته به شما کمک فراوانی میکند.
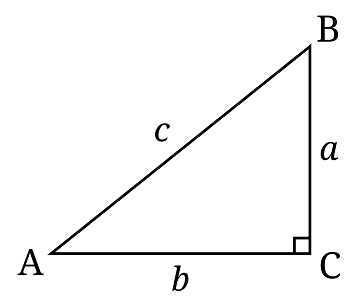
مثلث متساوی الاضلاع: این مثلث دارای سه ضلع مساوی و سه زاویه مساوی است. به این صورت که اگر اندازه یکی از اضلاع مثلث داده شد و در سوال قید شد که مثلث متساوی الاضلاع است، شما متوجه می شوید بقیه اضلاع نیز همین اندازه هستند. همچنین هر سه زاویه مساوی هستند که طبق قانون مجموع زوایای داخلی 180 درجه است هر زاویه در این نوع مثلث 60 درجه خواهد بود.
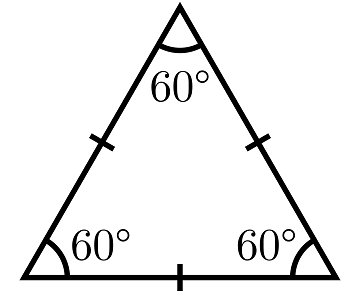
مثلث متساوی الساقین: این مثلث همانطور که از نامش پیداست دارای دو ضلع مساوی و دو زاویه پای ساق مساوی است. یعنی در این مثلث دو ساق با هم مساوی هستند و دو زاویه مجاور این ساق ها نیز با هم مساوی میشوند.
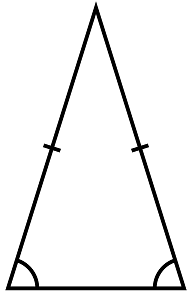
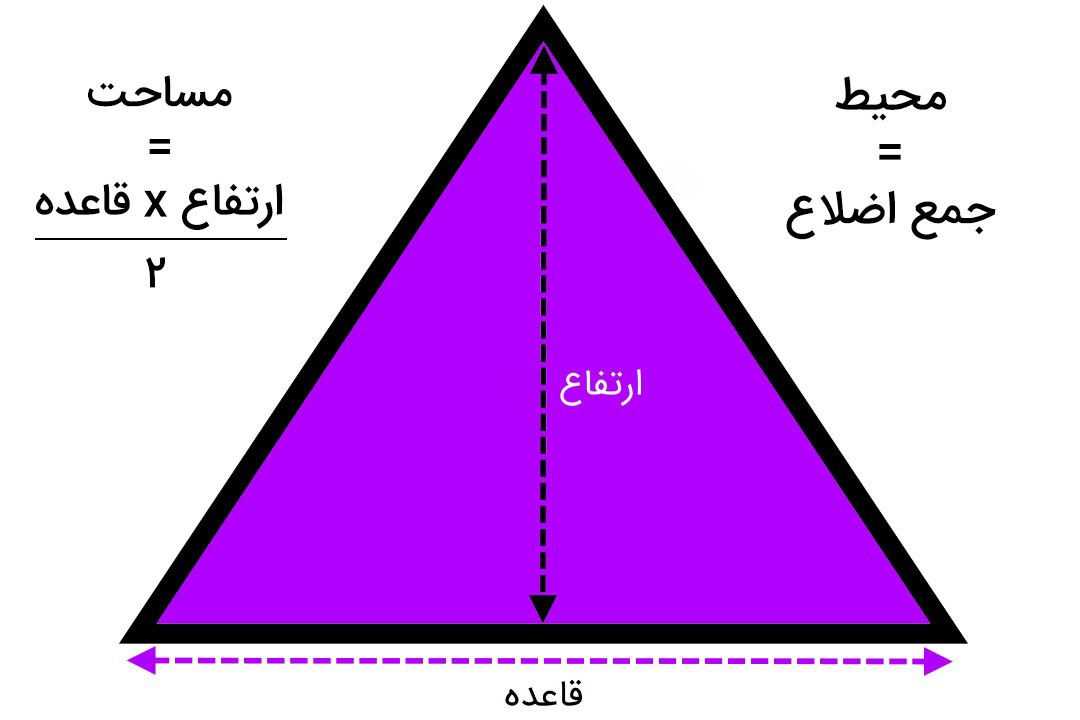
- محیط مثلث: جمع سه ضلع با یکدیگر
- مساحت مثلث: قاعده ضرب در ارتفاع تقسیم بر2
مطلب پیشنهادی: سبک های یادگیری
دنیای چهارضلعی ها
مربع
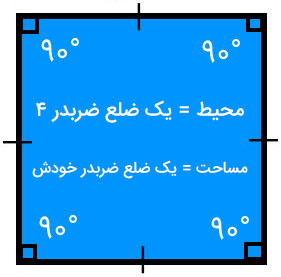
چهار ضلع مساوی، چهار زاویه مساوی و90 درجه، دارای چهار گوشه و 2 قطر که در وسط شکل یکدیگر را قطع می کنند و با هم مساوی هستند. در این شکل قطرها نیمساز زاویه ها هستند و در محل برخورد قطرها نصف می شوند و هم اندازه هستند.
- محیط مربع: یک ضلع ضرب در چهار
- مساحت مربع: یک ضلع ضرب در خودش
مستطیل
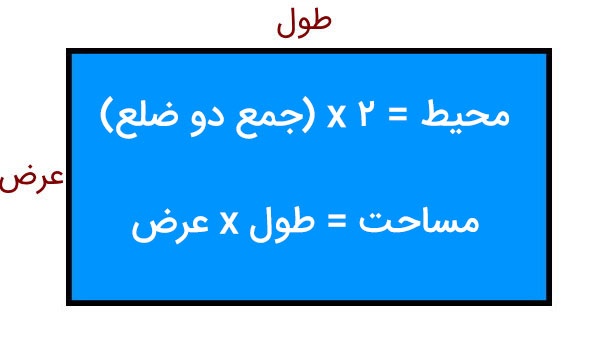
دارای چهار زاویه قائمه، ضلع های روبرو با هم مساوی و موازی هستند. دارای دو قطر که نیمساز زوایای داخلی مستطیل نیستند.
- محیط مستطیل: جمع طول و عرض ضرب در 2
- مساحت مستطیل: طول ضرب در عرض
متوازی الاضلاع
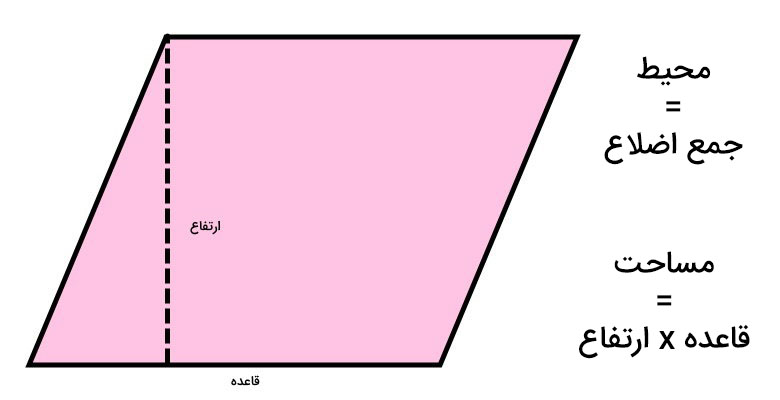
هر دو ضلع روبه رو موازی و مساوی هستند. دارای دو قطر می باشد که یکدیگر را نصف و قطع می کنند. زاویه های مجاور با هم مکمل و زاویه های مقابل با هم برابرند. این شکل و فرمول های آن مربوط به پایه چهارم ابتدایی می باشند.
- محیط متوازی الاضلاع: جمع دو ضلع ضرب در 2
- مساحت متوازی الاضلاع: قاعده ضرب در ارتفاع
لوزی
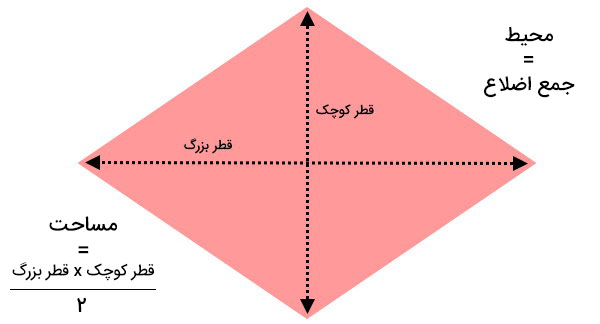
ضلع های رو بروی هم با یکدیگر موازی هستند. قطرها نیمساز زاویه ها هستند. قطرها در وسط یکدیگر را قطع میکنند. قطرها در برخورد با هم یکدیگر را نصف می کنند. فرمول مساحت این شکل در پایه پنجم ابتدایی به دانش آموزان آموزش داده میشود.
نکته: لوزی که زوایای آن 90 درجه باشد مربع است.
نکته: مجموع زوایای داخلی چهار ضلعی ها همگی 360 درجه است. از این نکته به فراوانی در حل سوالات استفاده می شود.
- محیط لوزی: جمع ضلع ها با یکدیگر
- مساحت لوزی: قطر بزرگ ضرب در قطر کوچک تقسیم بر2
ذوزنقه
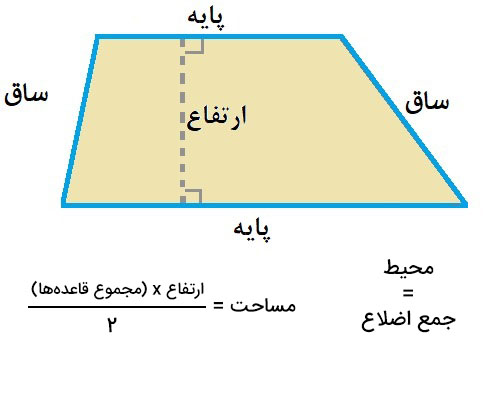
این شکل دارای دو ضلع موازی اما نامساوی است که به آنها قاعده ی کوچک و قاعده بزرگ ذوزنقه می گوییم. دو ضلع دیگر این شکل با هم موازی نیستند اما اگر با یکدیگر هم اندازه باشند ذوزنقه ما، ذوزنقه متساوی الساقین خوانده می شود. هر دو زاویه طرفین شکل با هم مکمل هستند. ذوزنقه دارای دو قطر است که یکدیگر را قطع می کنند اما نصف نمیکنند. محیط این شکل که با جمع اندازه ضلع ها به دست می آید، اما مساحت ذوزنقه و فرمول آن در مقطع پنجم ابتدایی آموزش داده می شود.
محیط ذوزنقه: جمع ضلع ها با هم
مساحت ذوزنقه: مجموع قاعده بزرگ و قاعده کوچک ضرب در ارتفاع تقسیم بر2
دایره
دایره شکلی است که دارای بی شمار ضلع است و این ضلع ها انقدر به هم نزدیک شده اند که تبدیل به خط خمیده شده اند و تشکیل دایره می دهند. دایره دارای بیشمار نقاط مقابل یکدیگر است پس بیشمار قطر دارد. البته در دایره ذکر این نکته ضروری به نظر می رسد که ما به خطی قطر می گوییم که حتما از مرکز دایره عبور کرده باشد. همچنین دارای بیشمار شعاع می باشد که در ادامه تعریف آن را خواهیم گفت. دایره دارای یک مرکز اصلی است که در وسط ترین نقطه آن قرار دارد و فاصله این نقطه از تمام نقاط روی محیط دایره به یک اندازه می باشد. آموزش محیط دایره در پایه پنجم برای دانش آموزان اتفاق می افتد و مساحت دایره در مقطع ششم ابتدایی آموزش داده می شود.
شعاع دایره: خطی که یک نقطه روی محیط دایره را به مرکز دایره وصل می کند، شعاع دایره گفته می شود که در محاسبه محیط و مساحت نیز مهم است.
نکته: شعاع دایره نصف قطر آن است.
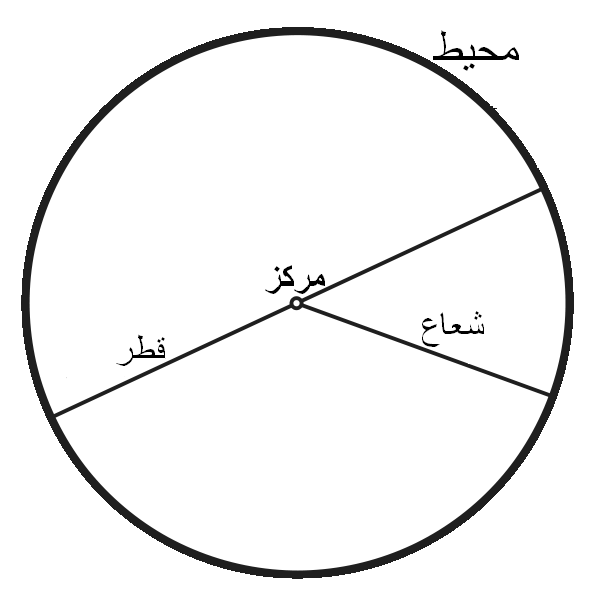
- محیط دایره: قطر ضرب در عدد پی
- مساحت دایره: شعاع ضرب در شعاع ضرب درعدد پی

رابطه و قانون تعداد ضلع ها و زاویه ها
در دوم ابتدایی کتاب ریاضی سوالاتی را مطرح می کند که در آن ها از بچه ها میخواهد تا با داشتن تعداد ضلعها تعداد زاویه ها که اصطلاحا در دوم ابتدایی گوشه نامیده می شود را بگویند که این بسیار آسان است به تعداد اضلاع زاویه یا گوشه وجود دارد. مثلا مثلث سه ضلع دارد پس سه زاویه هم دارد.
زوایای مکمل و متمم
تعریف زاویه مکمل
دو زاویه ای که جمع آنها به 180 درجه میرسد مکمل یکدیگر خوانده می شوند.
تعریف زاویه متمم
دو زاویه ای که جمع آنها به 90 درجه برسد متمم خوانده میشوند.
این مطالب تقریبا مقدار زیادی از دانش هندسه پایه هستند که درمقطع ابتدایی به دانش آموزان آموزش داده خواهند شد. امیدوارم برای شما مفید باشند.


سمیه پناهی
۱۴۰۴/۱۰/۱۷عالی